-
庞加莱定理 编辑
在一个封闭系统中,任何粒子在经过一个漫长的时间之后必然能无限接近其初始位置(但是不能回到原来位置,只能无限接近),尽管这个时间的长度远远超出我们所能想,但是它必然会实现。这样一个周期就称为一个庞加莱回归。2018年3月。维也纳大学的研究人员成功在一套多粒子量子系统中证实了一种“庞加莱回归”现象。研究结果已在《科学》期刊上发表。
中文名:庞加莱定理
外文名:Poincare's theorem
提出者:J.-H.庞加莱
提出时间:1890年
应用学科:热力学
1871年,James Clerk Maxwell首先对热力学第二法则导出的“热寂理论(热寂论)”发起诘难。
在James Clerk Maxwell之后更有科学家对热力学第二法则本身产生质疑,但是却苦于找不出熵恒增(熵恒增定律)的破绽。1895年。Jules Henri Poincaré(庞加莱)历史性地证明了庞加莱回归。
 庞加莱定理
庞加莱定理
由此导致他证明了下述庞加莱回归定理:设T为概率空间(X,.},川上的保测变换,对任意AE.}?,令A。一{x二〔A,且存在无限多个nEZ+,使T"(二)〔A},则A} E .-}且}(Ao)=}<A).根据上述定理,当X为可分度量空间卜了为其波莱尔。代数时,则({xw(x)})=0,即几乎所有点都是回归的。
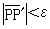
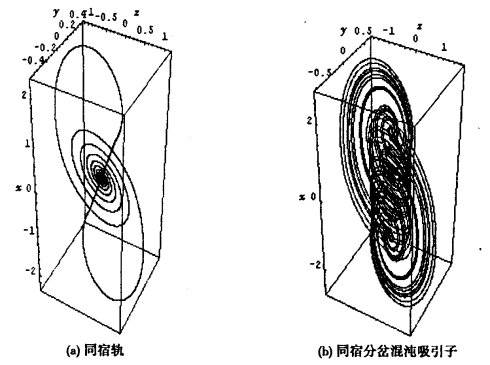
由此定理可以看出运动的可复性。因为从中可以得到结论:放在封闭容器内的任何一个力学体系经过足够长的时间后,总要回复到任意接近初始状态的那个状态上。由此可见,当H函数随时间单调地减少以后,只要经过足够长的时间,它将回复到初始的数值。这个结论似乎同宏观不可逆性相抵触,同玻耳兹曼H定理相矛盾。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。