数学上，相似性指两个图形的形状完全相似。若存在两个点的集，其中一个能透过放大缩小、平移或旋转等方式变成另一个，就说它们具有相似性。相似性所属现代词，指的是复杂系统的总体与部分,这部分与那部分之间的精细结构或性质所具有的。

相似性

分形思想的根源可以追溯到公元17世纪，而对分形使用严格的数学处理则始于一个世纪后卡尔·魏尔施特拉斯、格奥尔格·康托尔和费利克斯·豪斯多夫对连续而不可微函数的研究。但是分形（fractal）一词直到1975年才由本华·曼德博创造出，来自拉丁文frāctus，有“零碎”、“破裂”之意。一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统。

分形有几种类型，可以分别依据表现出的精确自相似性、半自相似性和统计自相似性来定义。虽然分形是一个数学构造，它们同样可以在自然界中被找到，这使得它们被划入艺术作品的范畴。分形在医学、土力学、地震学和技术分析中都有应用。

精确自相似

这是最强的一种自相似，分形在任一尺度下都显得一样。由 迭代函数系统定义出的分形通常会展现出精确自相似来。

半自相似

这是一种较松的自相似，分形在不同尺度下会显得大略（但非精确）相同。半自相似分形包含有整个分形扭曲及退化形式的缩小尺寸。由 递推关系式定义出的分形通常会是半自相似，但不会是精确自相似。

统计自相似

这是最弱的一种自相似，这种分形在不同尺度下都能保有固定的数值或统计测度。大多数对“分形”合理的定义自然会导致某一类型的统计自相似（分形维数本身即 是个在不同尺度下都保持固定的数值测度）。随机分形是统计自相似，但非精确及半自相似的分形的一个例子。

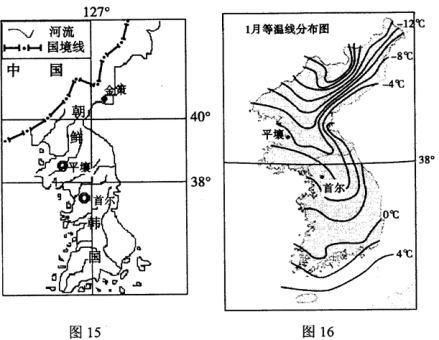结构相似性

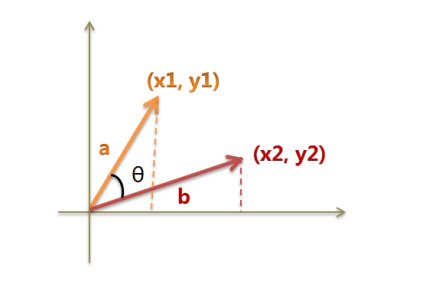余弦相似性

值得注意的是余弦相似度可以用在任何维度的向量比较中，它尤其在高维正空间中的利用尤为频繁。例如在信息检索中，每个词条拥有不同的度，一个文档是由一个由有权值的特征向量表示的，权值的计算取决于词条在该文档中出现的频率。余弦相似度因此可以给出两篇文档其主题方面的相似度。

另外，它通常用于文本挖掘中的文件比较。此外，在数据挖掘领域中，用它来衡量集群内部的凝聚力。

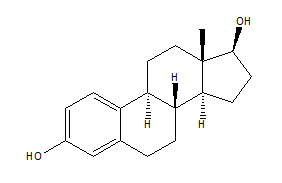化学相似性

化学相似性（或分子相似性）的概念是化学信息学中（chemoinformatics）最重要的主题之一。在化合物性质预测或设计特定性质化合物的现代研究中，化学相似性都有重要的作用。而有些药物设计研究会利用大型化学品数据库进行筛选，也和化学相似性有关。上述研究的基础是Johnson和Maggiora的相似性质定律：“相似的化合物会有相似的性质”。

遗传相似性

这些数据来源于不同的二级数据源，并用不同的方法获得（例如DNA-DNA杂交或序列比对），这可能导致相同物种间的比较得到不同的结果。因此，这些数据应该仅仅用作大致相似性。