-
对偶图 编辑
对偶图
对偶图是与平面图相伴的一种图。对于给定平面图G=〈V，E〉，设G的面为F₁，F₂，…，Fₑ，当图G*满足如下条件时，则图G*=〈V*,E*〉称为G的对偶图：①对G的每个面Fₒ，内部任选一点v*ₒ∈V*； ②对Fₒ，Fₓ的每一条公共边界eₔ，vₒ*与vₓ*间有一条边eₔ*，并且eₔ*与eₔ交于一点； ③当且仅当eₔ仅是一个面Fₒ的边界时，vₒ*有一个环(自回路)，eₒ*与eₔ相交。
设G是平面图，在图G的每个面中指定一个新结点，对两个面公共的边，指定一条新边与其相交。由这些新结点和新边组成的图称为G的对偶图
例1%20图1的图(b)中的虚线是图(a)的对偶图。%20
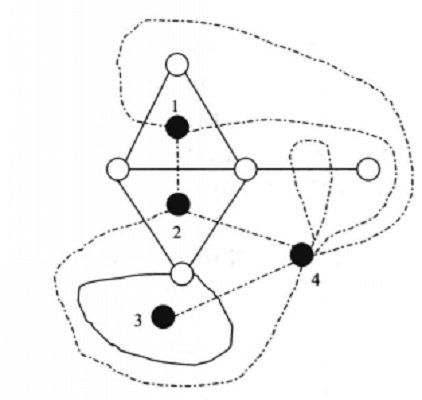
例2 图2的图(b)中的虚线是图(a)的对偶图。
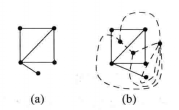图2
给定平面图G，用如下的方法构造G的对偶图
1)在G的每一个面
2)若
3)若
（1）如果G是一个连通图且G'是G的对偶图，则G%20也是G'的对偶图。%20
（2）同构平面图的对偶图不一定是同构的。G的对偶图的对偶图也不一定与G同构。
（3）设n、e、f分别为平面图G的结点数、边数和面数，
（4）若与G同构，称G自对偶(self%20dual)。
（5）任何平面图G的对偶图都是连通的。
（6）若边e为G中的环，则它对应的边为的割边；若边e为G中的割边，则为的环；
（7）G存在唯一的对偶图；
如图3、图4所示图G，以虚线为边的图即为G的对偶图。
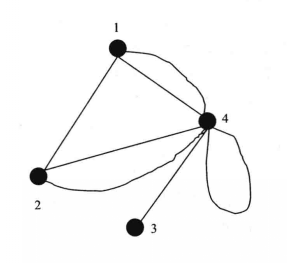图4
1、本站所有文本、信息、视频文件等，仅代表本站观点或作者本人观点，请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来，仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷，本站不承担任何责任。
4、如有侵犯你版权的，请来信（邮箱:baike52199@gmail.com）指出，核实后，本站将立即删除。
