抛物面，是指抛物线旋转180°所得到的面。数学上的抛物线就是同一平面上到定点（焦点）的距离与到定直线（准线）的距离相等的点的集合 。

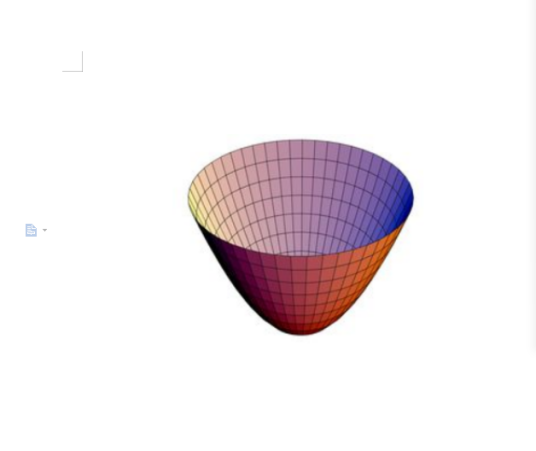
抛物面是二次曲面的一种。抛物面有两种：椭圆抛物面和双曲抛物面。

中文名：抛物面

外文名：paraboloid

定义：抛物线旋转180°所得到的面

应用：车灯、手电筒以及雷达

抛物线：到定点与到定直线距离相等点集合

标准方程：x^2+y^2-z/a^2=0

抛物面是二次曲面的一种。抛物面有两种：椭圆抛物面和双曲抛物面。椭圆抛物面在笛卡儿坐标系中的方程为：

双曲抛物面在笛卡儿坐标系中的方程为：

在车灯、手电筒等照明器具以及雷达中应用得非常多。它们的反光面或者反射面都是抛物面。

当a = b时，曲面称为旋转抛物面，它可以由抛物线绕着它的轴旋转而成。它是抛物面反射器的形状，把光源放在焦点上，经镜面反射后，会形成一束平行的光线。反过来也成立，一束平行的光线照向镜面后，会聚集在焦点上。

椭圆抛物面的参数方程为：

高斯曲率为：

平均曲率为：

它们都是正数，在顶点处最大，越远离顶点曲率越小，并趋近于零。

双曲抛物面的参数方程为：

高斯曲率为：

平均曲率为：