拓扑学(topology)，是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。在拓扑学里，重要的拓扑性质包括连通性与紧致性。拓扑英文名是Topology，直译是“地志学”，最早指研究地形、地貌相类似的有关学科。拓扑学是由几何学与集合论里发展出来的学科，研究空间、维度与变换等概念。这些词汇的来源可追溯至哥特佛莱德·莱布尼茨，他在17世纪提出“位置的几何学”（geometria situs）和“位相分析”（analysis situs）的说法。莱昂哈德·欧拉的柯尼斯堡七桥问题与欧拉示性数被认为是该领域最初的定理。拓扑学的一些内容早在十八世纪就出现了，后来在拓扑学的形成中占着重要的地位。

中文名：拓扑学

外文名：Topology

创立者：亨利·庞加莱

分类：数学

相关：七桥问题，四色问题

提出：莱布尼茨

拼音：tuò pū xué

有关拓扑学的一些内容早在十八世纪就出现了。那时候发现一些孤立的问题。后来在拓扑学的形成中占着重要的地位。譬如哥尼斯堡七桥问题、多面体的欧拉定理、四色问题等都是拓扑学发展史的重要问题。

七桥问题

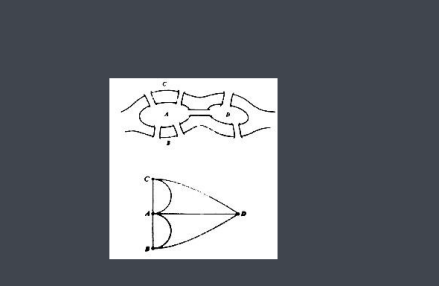图1 七桥问题

18世纪著名古典数学问题之一。在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来（如图1）。问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点？欧拉于1736年研究并解决了此问题，他把问题归结为如图1的“一笔画”问题，证明上述走法是不可能的。

有关图论研究的热点问题。18世纪初普鲁士的哥尼斯堡，有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来。有个人提出一个问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。后来大数学家欧拉把它转化成一个几何问题——一笔画问题。他不仅解决了此问题，且给出了连通图可以一笔画的充要条件是：奇点的数目不是0个就是2个（连到一点的数目如是奇数条，就称为奇点，如果是偶数条就称为偶点，要想一笔画成，必须中间点均是偶点，也就是有来路必有另一条去路，奇点只可能在两端，因此任何图能一笔画成，奇点要么没有要么在两端）

欧拉定理

图2 拓扑学

在拓扑学的发展历史中，还有一个著名而且重要的关于多面体的定理也和欧拉有关。这个定理内容是：如果一个凸多面体的顶点数是v、棱数是e、面数是f，那么它们总有这样的关系：f+v-e=2。

根据多面体的欧拉定理，可以得出这样一个有趣的事实：只存在五种正多面体。它们是正四面体、正六面体、正八面体、正十二面体、正二十面体。

四色问题

著名的“四色问题”也是与拓扑学发展有关的问题，又称四色猜想。1852年，毕业于伦敦大学的弗南西斯.格思里来到一家科研单位搞地图着色工作时发现：每幅地图都可以用四种颜色着色，使得有共同边界的国家都被着上不同的颜色。

1872年，英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题，于是四色猜想成了世界数学界关注的问题。1976年，美国数学家阿佩尔与哈肯在美国伊利诺斯大学的两台不同的电子计算机上，用了1200个小时，做了100亿种判断，终于完成了四色定理的证明。不过不少数学家并不满足于计算机取得的成就，他们认为应该有一种简捷明快的书面证明方法。

Topology原意为地貌，起源于希腊语Τοπολογ。形式上讲，拓扑学主要研究“拓扑空间”在“连续变换”下保持不变的性质。简单的说，拓扑学是研究连续性和连通性的一个数学分支。

拓扑学起初叫形势分析学，是德国数学家莱布尼茨1679年提出的名词。十九世纪中期，德国数学家黎曼在复变函数的研究中强调研究函数和积分就必须研究形势分析学。从此开始了现代拓扑学的系统研究。

等价

在拓扑学里不讨论两个图形全等的概念，但是讨论拓扑等价的概念。比如，圆和方形、三角形的形状、大小不同，但在拓扑变换下，它们都是等价图形；足球和橄榄球，也是等价的----从拓扑学的角度看，它们的拓扑结构是完全一样的。

而游泳圈的表面和足球的表面则有不同的拓扑性质，比如游泳圈中间有个“洞”。在拓扑学中，足球所代表的空间叫做球面，游泳圈所代表的空间叫环面，球面和环面是“不同”的空间。

性质

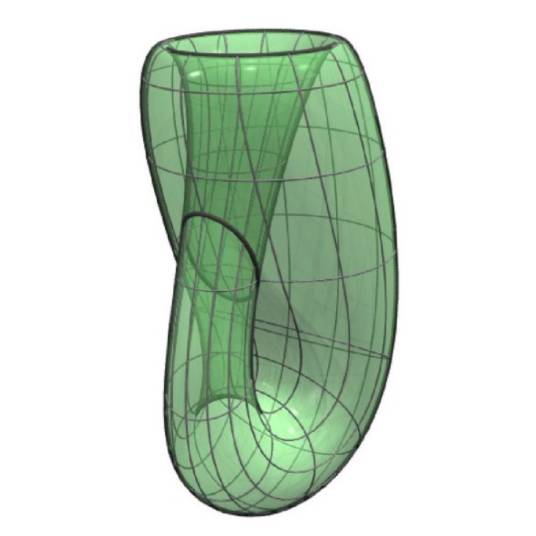
图3 莫比乌斯曲面

“连通性”最简单的拓扑性质。上面所举的空间的例子都是连通的。而“可定向性”是一个不那么平凡的性质。我们通常讲的平面、曲面通常有两个面，就像一张纸有两个面一样。这样的空间是可定向的。

而德国数学家莫比乌斯（1790～1868）在1858年发现了莫比乌斯曲面。这种曲面不能用不同的颜色来涂满。莫比乌斯曲面是一种“不可定向的”空间。可定向性是一种拓扑性质。这意味着，不可能把一个不可定向的空间连续的变换成一个可定向的空间。

萌芽

拓扑学起初叫形势分析学，这是德国数学家莱布尼茨1679年提出的名词。欧拉在1736年解决了七桥问题，1750年发表了多面体公式；高斯1833年在电动力学中用线积分定义了空间中两条封闭曲线的环绕数。Topology这个词是由J.B.利斯廷提出的（1847），源自希腊文τόπος和λόγος（“位置”和“研究”）。这是拓扑学的萌芽阶段。

1851年，德国数学家黎曼在复变函数的研究中提出了黎曼面的几何概念，并且强调为了研究函数、研究积分，就必须研究形势分析学。黎曼本人解决了可定向闭曲面的同胚分类问题。

组合拓扑学的奠基人是法国数学家庞加莱。他是在分析学和力学的工作中，特别是关于复函数的单值化和关于微分方程决定的曲线的研究中，引向拓扑学问题的。他的主要兴趣在流形。在1895～1904年间，他创立了用剖分研究流形的基本方法。他引进了许多不变量：基本群、同调、贝蒂数、挠系数，探讨了三维流形的拓扑分类问题，提出了著名的庞加莱猜想。

拓扑学的另一渊源是分析学的严密化。实数的严格定义推动康托尔从1873年起系统地展开了欧氏空间中的点集的研究，得出许多拓扑概念，如聚点（极限点）、开集、闭集、稠密性、连通性等。在点集论的思想影响下，分析学中出现了泛函（即函数的函数）的观念，把函数集看成一种几何对象并讨论其中的极限。这终于导致抽象空间的观念。

点集拓扑

图4 拓扑学

最早研究抽象空间的是M.-R.弗雷歇。他在1906年引进了度量空间的概念。F.豪斯多夫在《集论大纲》（1914）中用开邻域定义了比较一般的拓扑空间，标志着用公理化方法研究连续性的一般拓扑学的产生。随后波兰学派和苏联学派对拓扑空间的基本性质（分离性、紧性、连通性等）做了系统的研究。经过20世纪30年代中期起布尔巴基学派的补充（一致性空间、仿紧性等）和整理，一般拓扑学趋于成熟，成为第二次世界大战后数学研究的共同基础。

欧氏空间中的点集的研究，一直是拓扑学的重要部分，已发展成一般拓扑学与代数拓扑学交汇的领域，也可看作几何拓扑学的一部分。50年代以来，即问两个映射，以R.H.宾为代表的美国学派的工作加深了对流形的认识，是问两个给定的映射是否同伦，在四维庞加莱猜想的证明中发挥了作用。从皮亚诺曲线引起的维数及连续统的研究，习惯上也看成一般拓扑学的分支。

代数拓扑

L.E.J.布劳威尔在1910～1912年间提出了用单纯映射逼近连续映射的方法， 许多重要的几何现象，用以证明了不同维的欧氏空间不同胚，它们就不同胚。引进了同维流形之间的映射的度以研究同伦分类，并开创了不动点理论。他使组合拓扑学在概念精确、论证严密方面达到了应有的标准。紧接着，J.W.亚历山大1915年证明了贝蒂数与挠系数的拓扑不变性。

随着抽象代数学的兴起，1925年左右A.E.诺特提议把组合拓扑学建立在群论的基础上，在她的影响下H.霍普夫1928年定义了同调群。从此组合拓扑学逐步演变成利用抽象代数的方法研究拓扑问题的代数拓扑学。如维数、欧拉数，S.艾伦伯格与N.E.斯廷罗德1945年以公理化的方式总结了当时的同调论，后写成《代数拓扑学基础》

2016年10月4日下午5点45分，2016年诺贝尔物理学奖揭晓，三位英美科学家David J. Thouless， F. Duncan M. Haldane，J. Michael Kosterlitz获奖。获奖理由是“理论发现拓扑相变和拓扑相物质”。其中，David J. Thouless独享一半奖金，F. Duncan M. Haldane与J. Michael Kosterlitz分享另一半奖金。

David J. Thouless,1934年出生于英国贝尔斯登，1958年从美国康奈尔大学获得博士学位。现为美国华盛顿大学荣誉退休教授。

F. Duncan M. Haldane，1951年出生于英国伦敦，1978年从英国剑桥大学获得博士学位。现为美国普林斯顿大学物理学教授。

J. Michael Kosterlitz，1942年出生于英国阿伯丁，1969年从英国牛津大学获得博士学位。现为美国布朗大学物理学教授。

关于中国的第一篇拓扑学论文有两种观点：一种认为1925或1926年俞大维发表了第一篇拓扑学论文，这源自李仲珩(李达)1944年在《科学》第3期发表的《三十年来中国的算学》；另一种否定前者，提出1931年江泽涵发表了第一篇拓扑学论文。