范德华方程是荷兰物理学家范德瓦耳斯（van der Waals，又译“范德华”、“凡德瓦耳”）于1873年提出的一种实际气体状态方程。范德华方程是对理想气体状态方程的一种改进，特点在于将被理想气体模型所忽略的气体分子自身大小和分子之间的相互作用力考虑进来，以便更好地描述气体的宏观物理性质。

中文名：范德华方程

外文名：Van der Waals law calculator

时间：1873年

类型：一种实际气体状态方程

提出：范德华

简称：范氏方程

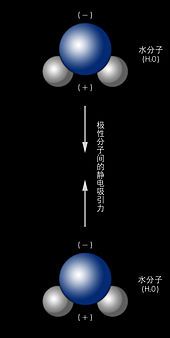
范氏方程

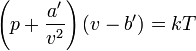范德瓦耳斯方程

p为气体的压强

a'为度量分子间引力的唯象参数

b'为单个分子本身包含的体积

v为每个分子平均占有的空间大小（即气体的体积除以总分子数量）;

k为玻尔兹曼常数

T绝对温度

更常用的形式为：

(p+an^2/V^2)(V-nb)=nRT

在第二个方程里

V为总体积

n为摩尔量（number of moles）

a为度量分子间引力的参数

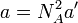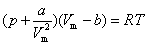方程

方程

NA为阿伏加德罗常数.

下表列出了部分气体的a，b的值

在上述方程中必须严格区分总体平均性质和单个分子的性质。譬如，第一个方程中的v是每个分子平均占有空间的大小（可以理解成分子平均“势力范围”的大小），而b'则为单个分子本身“包含”的体积（若为单原子分子如稀有气体，b'就是原子半径内包含的体积）。

按照下面的方式定义约减变量（亦称折合变量，就是把变量转换成其无量纲形式），其中下标R 表示约减变量，下标C 表示原变量的临界值：

pR=p/pC,

vR=v/vC,

Tr=T/Tc

式中pC=a/27b2，vC=3b，kTc=8a/27b

用约减变量代替原变量，范氏方程形式变为

（pR+3/vR^2)(vR-1/3)=(8/3)*TR

这就是范氏方程的不变形式，即这一形式不会因应用流体种类改变而改变。

上述方程的不变性质亦称对应态原理

但是，当描述对象处于状态参量空间(P,V,T)中气液相变区（即正在发生气液转变）时，对于固定的温度，气相的压强恒为所在温度下的饱和蒸气压，即不再随体积V（严格地说应该是单位质量气体占用的体积，即比容）变化而变化，所以这种情况下范氏方程不再适用。

(p+A)(V-b)=CT,

其中p为压强，V为比容，T为温度，A、B、C均为与对象相关的参数 。