衍射（英语：diffraction）是指波遇到障碍物时偏离原来直线传播的物理现象。在经典物理学中，波在穿过狭缝、小孔或圆盘之类的障碍物后会发生不同程度的弯散传播。假设将一个障碍物置放在光源和观察屏之间，则会有光亮区域与阴晦区域出现于观察屏，而且这些区域的边界并不锐利，是一种明暗相间的复杂图样。这现象称为衍射，当波在其传播路径上遇到障碍物时，都有可能发生这种现象。除此之外，当光波穿过折射率不均匀的介质时，或当声波穿过声阻抗（acoustic impedance）不均匀的介质时，也会发生类似的效应。在一定条件下，不仅水波、光波能够产生肉眼可见的衍射现象，其他类型的电磁波（例如X射线和无线电波等）也能够发生衍射。由于原子尺度的实际物体具有类似波的性质，它们也会表现出衍射现象，可以通过量子力学研究其性质。在适当情况下，任何波都具有衍射的固有性质。然而，不同情况中波发生衍射的程度有所不同。如果障碍物具有多个密集分布的孔隙，就会造成较为复杂的衍射强度分布图样。这是因为波的不同部分以不同的路径传播到观察者的位置，发生波叠加而形成的现象。衍射的形式论还可以用来描述有限波（量度为有限尺寸的波）在自由空间的传播情况。例如，激光束的发散性质、雷达天线的波束形状以及超声波传感器的视野范围都可以利用衍射方程来加以分析。

中文名：衍射

外文名：diffraction

创始人：a弗朗西斯科·格里马第/a

原理：波遇到障碍物时偏离原来直线传播

发表时间：1655年

包括：单缝衍射、圆孔衍射、圆板衍射

光的衍射效应最早是由弗朗西斯科·格里马第（Francesco Grimaldi）于1665年发现并加以描述，他也是“衍射”一词的创始人。这个词源于拉丁语词汇diffringere，意为“成为碎片”，即波原来的传播方向被“打碎”、弯散至不同的方向。格里马第观察到的现象直到1665年才被发表，这时他已经去世。他提出“光不仅会沿直线传播、折射和反射，还能够以第四种方式传播，即通过衍射的形式传播。”（"Propositio I. Lumen propagatur seu diffunditur non solum directe, refracte, ac reflexe, sed etiam alio quodam quarto modo, diffracte."）

英国科学家艾萨克·牛顿对这些现象进行了研究，他认为光线发生了弯曲，并认为光是由粒子构成。在19世纪以前，由于牛顿在学界的权威，光的粒子说在很长一段时间占有主流位置。这样的情况直到19世纪几项理论和实验结果的发表，才得以改变。1803年，托马斯·杨进行了一项非常著名的实验，这项实验展示了两条紧密相邻的狭缝造成的干涉现象，后人称之为“双缝实验”。在这个实验中，一束光照射到具有紧挨的两条狭缝的遮光挡板上，当光穿过狭缝并照射到挡板后面的观察屏上，可以产生明暗相间的条纹。他把这归因于光束通过两条狭缝后衍射产生的干涉现象，并进一步推测光一定具有波动的性质。奥古斯丁·菲涅耳则对衍射做了更多权威的计算研究，他的结果分别于1815年和1818年被发表，他提到“这样，我就展示了人们能够通过何种方式来构想光以球面波连续不断地传播出去……”（ "J'ai donc montré de quelle façon l'on peut concevoir que la lumière s'étend successivement par des ondes sphériques, ..."）

法国科学院曾经举办了一个关于衍射问题的有奖辩论会，菲涅耳赢得了这次辩论。作为反对光波动学说的其中一位，西莫恩·德尼·泊松提出，如果菲涅耳声称的结论是正确的，那么当光射向一个球的时候，将会在球后面阴影区域的中心找到亮斑。结果，评审委员会安排了上述实验，并发现了位于阴影区域中心的亮斑（它后来被称作泊松光斑）。这个发现极大地支持了菲涅耳的理论。 他的研究为克里斯蒂安·惠更斯发展的光的波动理论提供了很大的支持。他与杨的理论共同反驳了牛顿关于光是粒子的理论。

在对衍射现象的探索过程中，人们也不断积累了对于衍射光栅的认识。17世纪，苏格兰数学家、天文学家詹姆斯·格雷戈里（James Gregory）在鸟的羽毛缝间观察到了阳光的衍射现象。他是第一个发现衍射光栅原理的科学家。在1673年5月13日他写给约翰·科林斯（John Colins）的一封信中提到了此发现。1786年，美国天文学家戴维·里滕豪斯用螺丝和细线第一次人工制成了衍射光栅，细线的密度达到每英寸100线，他用这个装置成功地看到了阳光的衍射。1821年，约瑟夫·夫琅禾费利用相似的装置（每厘米127线）证明了托马斯·杨关于衍射的公式{φ10-φ20=2π/λ*（R1-R2）}，并对衍射进行了许多重要研究。1867年，刘易斯·卢瑟福（Lewis Morris Rutherfurd）采用水轮机作为动力进行刻线、制作光栅。后来的亨利·奥古斯塔斯·罗兰 改良了光栅的刻划技术，并在1882年发明了在凹形球面镜上进行刻划的凹面光栅。其后的罗伯特·伍德（Robert William Wood）改进了光栅的刻划形状，从而提高了光栅的衍射效率。近代的阿尔伯特·迈克耳孙提出利用干涉伺服系统控制光栅的刻划过程，于1948年实现了这一想法。20世纪下半叶，由于激光、光刻胶等新技术的出现，光栅制造技术取得很大的进步，制造成本显著降低，制造周期也得以缩短。

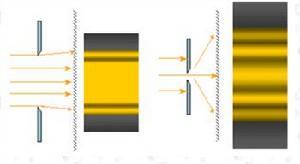衍射图样

如果采用单色平行光作为光源，则衍射后将产生干涉结果。相干波在空间某处相遇后，因位相不同，相互之间产生干涉作用，引起相互加强或减弱的物理现象。 衍射的结果是产生明暗相间的衍射花纹，代表着衍射方向（角度）和强度。根据衍射花纹可以反过来推测光源和光栅的情况。 为了使光能产生明显的偏向，必须使“光栅间隔”具有与光的波长相同的数量级。用于可见光谱的光栅每毫米要刻有约500条线 。

1912年，劳厄想到，如果晶体中的原子排列是有规则的，那么晶体可以当作是X射线的三维衍射光栅。X射线波长的数量级是10^-8cm,这与固体中的原子间距大致相同。果然试验取得了成功，这就是最早的X射线衍射。 显然，在X射线一定的情况下，根据衍射的花样可以分析晶体的性质。但为此必须事先建立X射线衍射的方向和强度与晶体结构之间的对应关系。

衍射示意图

光在传播路径中，遇到不透明或透明的障碍物或者小孔（窄缝），绕过障碍物，产生偏离直线传播的现象称为光的衍射。衍射时产生的明暗条纹或光环，叫衍射图样。

定义：光波遇到障碍物以后会或多或少地偏离几何光学传播定律的现象。

包括：单缝衍射、圆孔衍射、圆板衍射及泊松亮斑

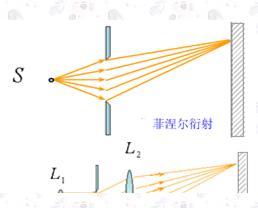菲涅尔衍射

产生衍射的条件是：由于光的波长很短，只有十分之几微米，通常物体都比它大得多，但是当光射向一个针孔、一条狭缝、一根细丝时，可以清楚地看到光的衍射。用单色光照射时效果好一些，如果用复色光，则看到的衍射图案是彩色的。

任何障碍物都可以使光发生衍射现象，但发生明显衍射现象的条件是“苛刻”的。

当障碍物的尺寸远大于光波的波长时，光可看成沿直线传播。注意，光的直线传播只是一种近似的规律，当光的波长比孔或障碍物小得多时，光可看成沿直线传播；在孔或障碍物可以跟波长相比，甚至比波长还要小时，衍射就十分明显。由于可见光波长范围为4×10∧-7m至7.7×10∧-7m之间，所以日常生活中很少见到明显的光的衍射现象。

惠更斯-菲涅尔原理

衍射

惠更斯提出，媒质上波阵面上的各点，都可以看成是发射子波的波源，其后任意时刻这些子波的波迹，就是该时刻新的波阵面。惠更斯－菲涅尔原理能定性地描述衍射现象中光的传播问题。菲涅尔充实了惠更斯原理，他提出波前上每个面元都可视为子波的波源，在空间某点P的振动是所有这些子波在该点产生的相干振动的叠加，称为惠更斯－菲涅尔原理。

菲涅尔衍射

指的是光源-衍射屏、衍射屏-接受屏之间的距离均为有限远，或其中之一为有限远的场合，或者说，球面波照明时在有限远处接收的是菲涅尔衍射场。 例如：圆孔衍射、圆屏衍射菲涅尔衍射、泊松亮斑。

夫琅禾费衍射

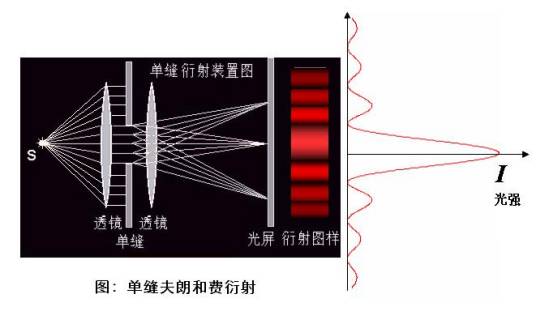
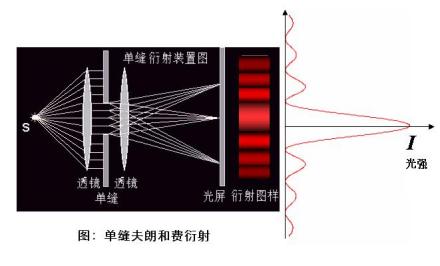单缝夫朗和费衍射

指的是衍射屏与两者的距离均是无限远的场合，或者说，平面波照明时在无穷远处接收的是夫琅禾费衍射场。 概略的看，菲涅尔衍射是近场衍射，而夫琅禾费衍射是远场衍射。不过，在成像衍射系统中，与照明用的点光源相共轭的像面上的衍射场也是夫琅禾费衍射场，此时，衍射屏与点光源或接收屏之距离在现实空间看，都是很近的。

红色激光的圆孔衍射图样

从理论上看，夫琅禾费衍射显然是菲涅尔衍射的一种特殊情形，而实际上却更为人们所重视，这是因为夫琅禾费衍射场的理论计算较为容易、应用价值又很大，而实验上又不难实现。尤其是，在现代变换光学中傅里叶光学的兴起，赋予经典夫琅禾费衍射以新的现代光学的意义——傅里叶光学是以夫琅禾费衍射衍射为枝杈生长起来的。

例如：单缝夫琅禾费衍射、矩孔和三角孔夫琅禾费衍射、圆孔夫琅禾费衍射

①狭缝衍射

X射线衍射仪

当狭缝很宽时，缝的宽度远远大于光的波长，衍射现象极不明显，光沿直线传播，在屏上产生一条跟缝宽度相当的亮线；但当缝的宽度调到很窄，可以跟光波相比拟时，光通过缝后就明显偏离了直线传播方向，照射到屏上相当宽的地方，并且出现了明暗相间的衍射条纹，狭缝越小，衍射范围越大，衍射条纹越宽。但亮度越来越暗。

试验：可以用游标卡尺调整到肉眼可辨认的最小距离，再通过此缝看光源

②小孔衍射

当孔半径较大时，光沿直线传播，在屏上得到一个按直线传播计算出来一样大小的亮光圆斑；减小孔的半径，屏上将出现按直线传播计算出来的倒立的光源的像，即小孔成像；继续减小孔的半径，屏上将出现明暗相间的圆形衍射光环。

应用射线概念分析电磁波衍射特性的渐近理论，简称 GTD。几何理论是单色波场方程的解在频率趋于无限时的极限,因而也是适合于高频情形的渐近解,而这种理论的基本思想是把均匀平面波在无限平界面上的反射和折射、在半无限楔形导体边缘上的衍射和沿圆柱导体表面的爬行波严格解的渐近式，应用于从点源发出的球面波或线源发出的柱面波在圆滑界面上的反射和折射、在弧形导体刃口上的衍射和沿导体凸表面的爬行，并把它作为问题的0阶段近解。

电脑模拟生成的红色激光的方孔衍射图样

衍射的几何理论最早是由J.B.凯勒于1957年提出来的，后来经许多人的工作而日趋完善，在处理很多异形物体的散射问题以及用数值计算解散射和衍射问题中得到应用。但是，因为严格解的渐近式在阴影区与照明区的过渡区域不能成立，所以在这个区域，GTD 不能应用，为了弥补这一缺陷，J.波斯马等人后来提出一致渐近理论 (UAT)。这个理论的基本思想是，给投射波乘以人为因子,使这因子在照明区内近于1而在阴影区内近于0,在过渡区内则随着场点趋近于照明区边界而无限增大。将这乘了因子的投射波与衍射波的渐近式相加能一致连续，这种理论也得到了广泛的应用。但是，它的基础仅仅是一个估值(ansatz),而且在刃口以及其他焦散线附近,它和 GTD同样不能应用。然而射线理论有很多优点，人们仍在探索改进的途径。