-
波动方程 编辑
波动方程或称波方程(英语:Wave equation) 由麦克斯韦方程组导出的、描述电磁场波动特征的一组微分方程,是一种重要的偏微分方程,主要描述自然界中的各种的波动现象,包括横波和纵波,例如声波、光波和水波。波动方程抽象自声学,电磁学,和流体力学等领域。
中文名:波动方程
外文名:Wave equation
所属学科:物理
应用学科:声学、电磁学、流体力学、电信
 波动方程的高频近似与辛几何
波动方程的高频近似与辛几何
历史上许多科学家,如达朗贝尔、欧拉、丹尼尔·伯努利和拉格朗日等在研究乐器等物体中的弦振动问题时,都对波动方程理论作出过重要贡献。
弦振动方程是在18世纪由达朗贝尔(d'Alembert)等人首先系统研究的,它是一大类偏微分方程的典型代表。
这里a通常是一个固定常数,也就是波的传播速率(对于空气中的声波大约是330米/秒, 参看音速)。对于弦的振动,这可以有很大的变化范围:在螺旋弹簧上(slinky),它可以慢到1米/秒。但若a作为波长的函数改变,它应该用相速度代替:
注意波可能叠加到另外的运动上(例如声波的传播在气流之类的移动媒介中)。那种情况下,标量u会包含一个马赫因子(对于沿着流运动的波为正,对于反射波为负)。
u%20=%20u(x,t),%20是振幅,在特定位置x和特定时间t的波强度的一个测量。对于空气中的声波就是局部气压,对于振动弦就是从静止位置的位移。
如,一维波动方程:
要决定
这样达朗贝尔公式变成了:
在经典的意义下,如果
一维情况的波动方程可以用如下方法推导:想象一个质量为m的小质点的队列,互相用长度h的弹簧连接。弹簧的硬度为k%20:
这里u%20(x)测量位于x的质点偏离平衡位置的距离。对于位于x+h的质点的运动方程是:
其中u(x)的时间依赖性变成显式的了。
上述式子称为广义波动方程或基尔霍夫方程。式中的“▽”称为哈密顿算符。在直角坐标系中
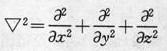 微分方程
微分方程
在自由空间或绝缘良好的介质中,电导率可以忽略不计,即σ=0,于是E和H的微分方程成为
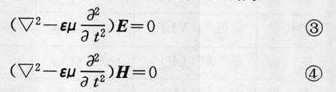 波动方程
波动方程
称为波动方程或达朗贝尔方程。
波动方程的解是在空间中一个沿特定方向传播的电磁波。对于电磁波传播问题的分析,都可归结为在给定的边界条件和初始条件下求波动方程的解。
标量波动方程 应用直角坐标系
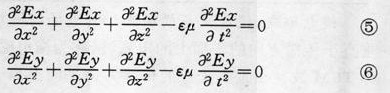 标量波动方程
标量波动方程
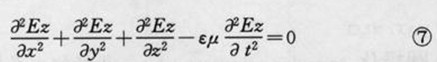 标量波动方程
标量波动方程
可以把③写成
即把矢量波动方程分解成三个标量波动方程,每个方程中只含一个知函数。但只有在应用直角坐标系时才能得到这样的结果,在其它坐标系中,通过分解而得的三个标量方程都具有复杂的形式。
亥姆霍兹方程 在场源按正弦规律随时间变化的条件下,场量也是同频率的正弦函数,可以用相量表示。由相量形式的麦克斯韦方程组出发,可以推导出相量形式的波动方程:
 亥姆霍兹方程
亥姆霍兹方程
式中:
 波动方程
波动方程
式⑧与⑨又称亥姆霍兹方程。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。






























