-
洛特卡-沃尔泰拉方程 编辑
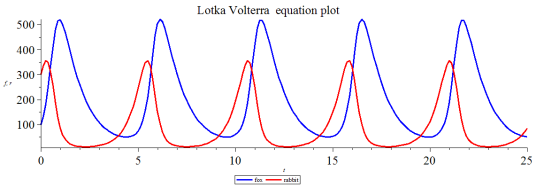
洛特卡-沃尔泰拉方程(Lotka-Volterra equations)别称掠食者—猎物方程。由两条一阶非线性微分方程组成。经常用来描述生物系统中,掠食者与猎物进行互动时的动力学,也就是两者族群规模的消长。此方程分别在1925年与1926年,由阿弗雷德·洛特卡与维多·沃尔泰拉独立发表。
中文名:洛特卡-沃尔泰拉方程
外文名:Lotka-Volterra equations
别名:掠食者—猎物方程
组成:两条一阶非线性微分方程
猎物族群的增值速度
第一式所表达的是猎物族群的增值速度:
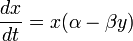 洛特卡-沃尔泰拉方程
洛特卡-沃尔泰拉方程
由上述的方程式可知:猎物族群规模的改变,源于本身受到捕食而产生的成长衰减。
掠食者族群的增值速度
第二式所表达的是掠食者族群的增值速度:
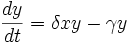 洛特卡-沃尔泰拉方程
洛特卡-沃尔泰拉方程
由上述的方程式可知:掠食者族群规模的改变,是猎食者族群的成长,减去其自然死亡的部分。
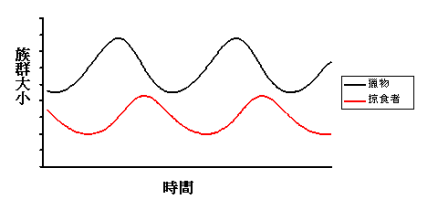 洛特卡-沃尔泰拉方程
洛特卡-沃尔泰拉方程
族群规模的平衡
族群的平衡会发生在族群大小不再变化的时候。例如:两条微分方程皆等于零的时候。
x(α − βy) = 0 − y(γ − δx) = 0 求解上述方程式的 x 与 y 可得:
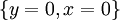 洛特卡-沃尔泰拉方程
洛特卡-沃尔泰拉方程
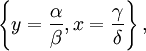 洛特卡-沃尔泰拉方程
洛特卡-沃尔泰拉方程
第一组解实际上是表示两个物种的灭绝,若是两个族群皆为零,则此状况将永久持续下去。第二组解表示一个不动点,意思是两个族群能够维持一个不为零的数量,并且在简单的模型中能够永久持续。系数 α, β, γ, 与 δ ,能够决定族群规模将在哪种情况下达成平衡状态。
不动点的稳定性
不动点的稳定性可以利用偏导数,将其以线性化方式呈现。
产生的掠食者猎物模型之雅可比矩阵如下:
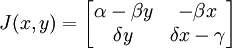 洛特卡-沃尔泰拉方程
洛特卡-沃尔泰拉方程
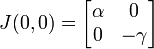 洛特卡-沃尔泰拉方程
洛特卡-沃尔泰拉方程
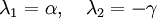 洛特卡-沃尔泰拉方程
洛特卡-沃尔泰拉方程
此不动点的稳定性相当重要,当处于稳定态的时候,非零的族群会趋向它。一些初始的族群可能会走向灭绝。然而当不动点位于原点时,也是一个鞍点,因此并不稳定。所以在此模型中,两个物种皆难以灭绝。除非以人为方式将猎物完全消灭,并使掠食者因饥荒而死亡。而若是将掠食者完全消灭,则猎物的族群增长情形,将会脱离此简单模型。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。