螺旋线属于空间曲线，它有圆柱螺旋线，圆锥螺旋线等多种形式。在建筑与机械工程中最常用的是圆柱螺旋线。数学中有各式各样富含诗意的曲线，螺旋线就是其中比较特别的一类。螺旋线这个名词来源于希腊文，它的原意是“旋卷”或“缠卷”。例如，平面螺旋便是以一个固定点开始向外逐圈旋绕而形成的曲线。在2000多年以前，古希腊数学家阿基米德就对螺旋线进行了研究。著名数学家笛卡尔于1638年首先描述了对数螺旋线，并且列出了螺旋线的解析式。更有趣的是瑞士数学家雅谷·伯努利，在逝世前请人在他的墓碑上刻了一条蜗牛屋形——对数螺旋线，并幽默地写上“我将按着原来的样子变化后复活”的墓志铭。

中文名：螺旋线

属性：空间曲线

名词来源：希腊文

按维度分类：二维螺旋线和三维螺旋线

最早研究时间：2000多年前

最早研究专家：古希腊数学家阿基米德

蜘蛛网是自然界中分布很广，而且给人印象深刻的一种螺旋结构。蜘蛛网的结构充分地说明了蜘蛛是一个多么了不起的、有着奇妙螺旋概念的生命 。

车前草的叶片也是螺旋状排列，其间夹角为137度、30度、38度。这样的叶序排列，可以使叶片获得最大的采光量，且得到良好的通风。其实，植物叶子在茎上的排列，一般都是螺旋状。此外，向日葵籽在盘上的排列也是螺旋式的 。

人的头发是从头皮毛囊中斜着生长出来的，它循着一定的方向形成旋涡状，这就是发旋，且有右旋和左旋之别。实际上，发旋是长在体表的毛旋，能使毛发顺着一定的方向生长。在野生兽类动物中，毛旋具有保护自身和适应环境的作用。它可使雨水顺着一定的方向淌掉，犹如披上了一件蓑衣一般；它们排列紧密，可避免有害昆虫的叮咬；除此，还有良好的保温作用。人类头发的这些作用虽然已退化到微不足道的地步，但其形式却保留了下来 。

特殊运动产生的螺旋线

1、一只蚂蚁以不变的速率，在一个均匀旋转的唱片中心沿半径向外爬行，结果蚂蚁本身就描绘出一条螺旋线 。

2、蝙蝠从高处往下飞，是按空间螺旋线——锥形螺旋线的路径飞行的 。

3、在大海上追逐逃跑的敌舰或缉捕走私船只，有时也要按着螺旋线路径追逐 。

4、星体的运行轨迹有的也是螺旋线。日本国家天文台的中井直政博士，在对银河系中部的气体密度进行了为期3年的观察研究后认为，银河系是呈螺旋状的，即星体以圆心呈螺旋状向外扩 。

二维螺旋线

1、阿基米德螺线

阿基米德螺线的极坐标方程式为：

阿基米德螺线

其中a和b均为实数。改变参数a相当于旋转螺线线，而参数b则控制相邻两条曲线之间的距离 。

阿基米德螺线的平面笛卡尔坐标方程式为 ：

从笛卡尔坐标系到极坐标系的变换%20：

从极坐标系到笛卡尔坐标系的变换%20：

2、费马螺线%20

费马螺线是等角螺线的一种，表达式：

费马螺线

3、等角螺线

等角螺线是指形式为：

的螺线%20。

等角螺线

4、双曲螺线

极坐标方程rθ=c，其中c为常数。直角坐标系中，x=c*cosθ\θ，y=c*sinθ\θ。因此可见渐近线为：y=c 。

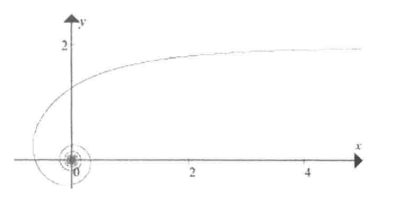双曲螺线

5、圆内螺线

在固定的大圆中内切一个运动的小圆，在小圆滚动的过程中，其上一个定点所形成的轨迹，,即为圆内螺线。该点会随着两圆半径比值的不同而出现不同轨迹 。

参数方程：x=cosθ+/ny=sinθ-/n 。

特别地，当小圆半径等于大圆的一半时，小圆每一点的轨迹都是大圆的一条直径；当小圆半径等于大圆的四分之一时，形成的轨迹则是星形线（见图三） 。

当改变大小圆半径比时，形成的轨迹见下图一 ：

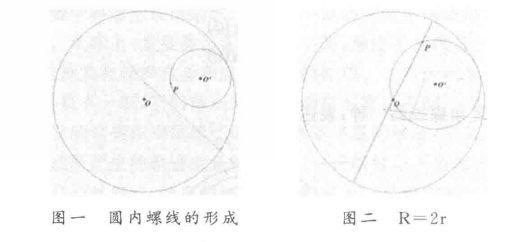图一、图二

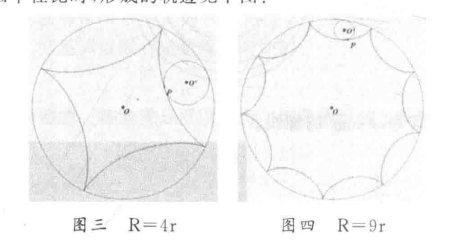图三、图四

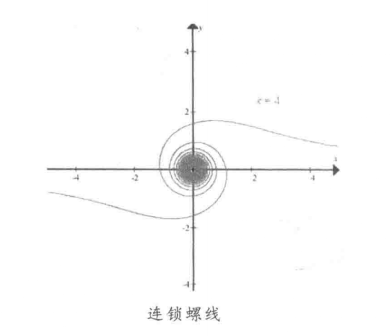
6、连锁螺线

连锁螺线，英文又称 Lituus螺线（如下图五所示），是由高中数学三种圆锥曲线的参数化、交互式而得到的 。

高中数学三种圆锥曲线的参数化是所有形式为rˆ2*Θ=k的螺线。连锁螺线rˆ2Θ=k满足：有一水平渐近线y=0 。

图五

注：公式中r为半径，Θ为夹角，k为斜率 。

7、柯奴螺线

柯奴螺线( KeNu spiral)，是一种数学领域的函数绘制的图形 。

三维螺旋线

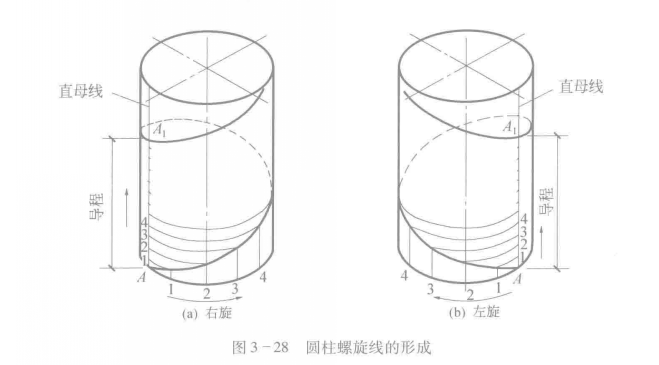
圆柱螺旋线

圆柱螺旋线 circular helix的正面投影是正弦曲线，水平投影是圆。根据动点旋转方向，螺旋线可分为左螺旋线和右螺旋线两种 。

圆柱螺旋线

当一动点沿圆柱面的直母线做匀速直线运动，而该母线又同时绕圆柱面的轴线作匀速回转运动时，该动点的轨迹为圆柱螺暶线。如图六所示 。

图六

其中，动点回转运动一周时沿轴向移动的直线距离称为导程(或螺距) 。

螺旋线有右旋和左旋之分 ：

1、右旋当轴线竖直时，螺旋线可见部分自左向右上升，称为右螺旋线 ；

2、 左旋当轴线竖直时，螺旋线可见部分自右向左上升，则称为左螺旋线 。

因此，确定圆柱螺旋线的三个要素是：圆柱面直径、导程、旋向 。

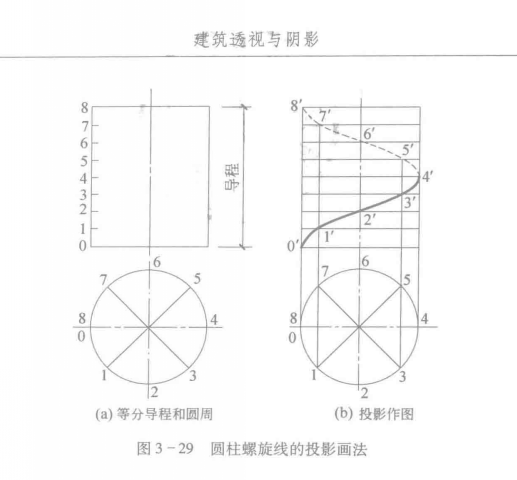
1、作圆柱面的两面投影，并将水平投影中的圆周和正面投影中所反映的导程分成相同的等份；然后，按右旋规律将圆周上的等分点编号，由下而上将导程线上的等分点编上相应的编号 ；

2、分别过正面投影和水平投影相同编号的等分点作水平线和竖直线，它们两两相交，得一系列交点1′、2′、3′、…、8′，将这些点依次光滑相连，区分可见性即得所求螺线的正面投影,其水平投影重合于圆柱面的积聚投影（圆周）上 。

图七