自旋网络编辑

图表

自旋网络

量子力学中，自旋网络是一种图表，用以表示粒子与量子场之间的的相互作用与状态。以数学的出发点来看，这些图案是一种简明方法，可代表多线性函数以及矩阵群众多表示之间的关联函数。此图案记号往往能简化计算，以其能代表复杂的函数。自旋网络的发明一般是归因于罗杰·彭罗斯于1971年的贡献，然而在此之前已有类似的图样方法。

1971年，罗杰·彭罗斯提出一种图形表示法，其中每个线段代表一个“单元”（基本粒子或粒子的复合系统）之世界线。三条线段汇聚在一个顶点。顶点可以诠释为一个事件；在此事件中，一个单元分裂成两个单元，或两个单元碰撞合而为一。当一图表中所有的线段都在顶点会合，则此图为“封闭自旋网络”。时间以单一方向行进，比如从图的底部走到图的顶部。然而在封闭自旋网络的例子，时间行进的方向对于计算不构成影响。

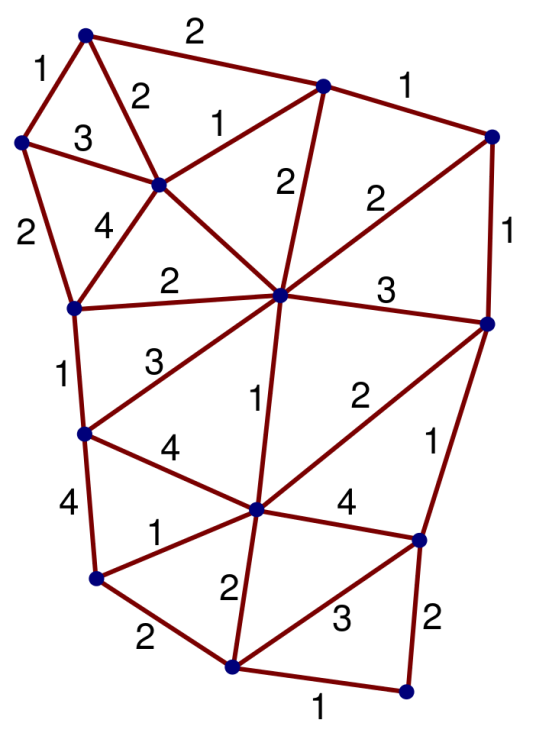
每一线段标上一个称作自旋量子数的整数。带有自旋数n的一个单元称作n-单元，其角动量为nħ，ħ是约化普朗克常数。光子、胶子等玻色子，其n为偶数；电子、夸克等费米子，其n为奇数。

给定一封闭自旋网络，则可计算出一个相应的非负整数的范数（norm）。范数可用来计算不同自旋值的概率。当一个自旋网络的范数是零，则其发生概率为零。当范数不为零时，在顶点处则有一些约束条件如下：

若有三个单元会合在一顶点，这三单元分别带有自旋量子数a、b、c，则必须满足

三角不等式：a必须小于或等于b+c，b必须小于或等于a+c，以及c必须小于或等于a+b。

费米子守恒（Fermion conservation）：a+b+c必须是偶数。

举例来说，a= 3,b= 4,c= 6的例子是不可能，因为3 + 4 + 6 = 13是奇数。a= 3,b= 4,c= 9也不可能，因为3 + 4 < 9。而a= 3,b= 4,c= 5则可行，因为3 + 4 + 5 = 12是偶数且满足三角不等式。

一些标记习惯会将整数标为半整数，约束条件则变成a+b+c的和要是整数。

自旋网络

1、本站所有文本、信息、视频文件等，仅代表本站观点或作者本人观点，请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来，仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷，本站不承担任何责任。
4、如有侵犯你版权的，请来信（邮箱:baike52199@gmail.com）指出，核实后，本站将立即删除。

下一篇宇宙监督假设

上一篇彭罗斯阶梯