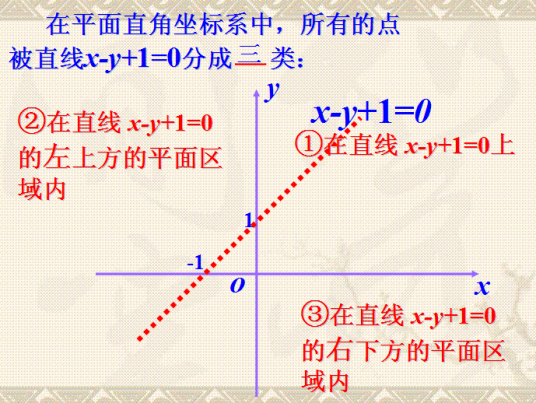
-
二元一次不等式 编辑
其中,两边的解析式的公共定义域称为不等式的定义域。
整式不等式:
整式不等式两边都是整式(即未知数不在分母上)。
一元一次不等式:含有一个未知数(即一元),并且未知数的次数是1次(即一次)的不等式。如3-X>0。
 直线与二元一次方程
直线与二元一次方程
(1)若A>0,B>0,则二元一次不等式Ax+By+C > 0表示直线Ax+By+C=0右上方的平面区域;
(2) A>0,B<0时,二元一次不等式Ax+ By+C >0表示直线Ax十By十C=0右下方的平面区域;
(3)A<0,B>0时,二元一次不等式Ax+By+C > 0表示直线Ax十By+C=0左上方的平面区域;
(4) A<0,B<0时,二元一次不等式Ax+ By+C > 0表示直线Ax+By+C=0左下方的平面区域;
(5)A=0,B>0时,二元一次不等式Ax+ By+C> 0表示直线
(6)A=0,B<0时,二元一次不等式Ax+%20By+C>%200表示直线
(7)A>0,B=0时,二元一次不等式Ax+%20By+C>%200表示直线
(8)A<0,B=0时,二元一次不等式Ax+%20By+C>0表示直线
用加减法解不等式的时候,不用去记住很多代入法要注意的小技巧,特别是考试时比较紧张,如果要记住太多很容易出错的。这种相加法,用熟之后过程可以不用这么繁复,可以少写一两步。
特别注意,根据不等式性质,不等号方向相同的两式子,只能相加,不能相减。
不等号方向相反时,两边才能相减,相减后的不等号方向与被减式相同。实际这跟两式相加一样的,只要把式子两边交换,">号"会变"<"号。不过这方法不严谨,只能用于选择填空,用于做大题会被判错的。而且比两式相加容易出错,所以一开始就乖乖做两式相加好了,等熟练了以后,做选择填空才用两式相减。
举例,2x+y>10……①
x+y<5………②
①-②,不等号取>%20可理解为:①+(-②)
(2x+y)-(x+y)>10-5
得x>5
将x>5带入②得,y<0
(a)若 2x> –12,则x> –6。
(b)若x+11>0 ,则x> –11。
(c)若 a< 2 < b,则(a– 2)(b– 2) < 0。
(d)若 a> b及 c> d,则a– c> b– d。
(e)若 a> b,则a– 4 > b– 4。
(f)若 a> 0 > b,则a> b。
答案:a对;b对;c对;d错;e对;f对;
B 在3x-y+5>0表示的直线y=3x+5上方还是下方区域?
答:A>0,B<0时,二元一次不等式Ax+ By+C >0表示直线Ax十By十C=0右下方的平面区域,此时A=3>0,B=-1<0,所以是下方区域。
1、本站所有文本、信息、视频文件等,仅代表本站观点或作者本人观点,请网友谨慎参考使用。
2、本站信息均为作者提供和网友推荐收集整理而来,仅供学习和研究使用。
3、对任何由于使用本站内容而引起的诉讼、纠纷,本站不承担任何责任。
4、如有侵犯你版权的,请来信(邮箱:baike52199@gmail.com)指出,核实后,本站将立即删除。