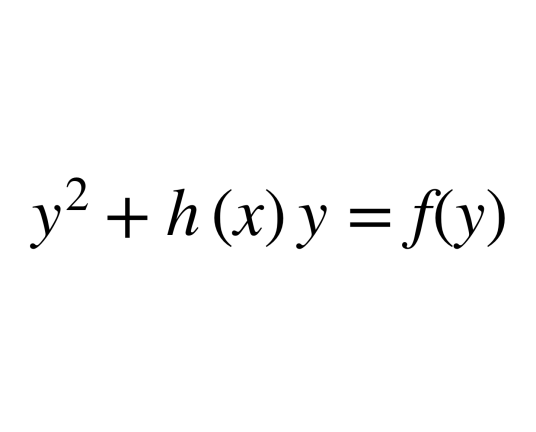设C是代数曲线，如果存在一个从C到射影直线P¹的二次覆盖(即全纯的2:1满射)，就称C是超椭圆曲线。超椭圆曲线在密码学中有很大的应用。美国华盛顿大学教授Neal Koblitz首先发明了超椭圆曲线密码。超椭圆曲线密码是利用超椭圆曲线C的Jacobian上的离散对数问题(HECDLP)的“不可行性”。但是只有亏格为2的超椭圆曲线密码的安全性能和椭圆曲线密码的安全性媲美。

中文名：超椭圆曲线

外文名：hyperelliptic curve

基本形式：y^2+h(x)y=f(y)

应用：超椭圆曲线密码

定义：设C是代数曲线，如果存在一个从C到射影直线P¹的二次覆盖(即全纯的2:1满射)

亏格为2的曲线必定是超椭圆曲线。 超椭圆曲线的曲线自同构群Aut(C)包含一个对合映射，从而诱导出到P¹的二次覆盖，对合映射的不动点恰好就是二次覆盖的分歧点。Aut(C)可以由P¹的曲线自同构群诱导出来。对于域K，亏格为g超椭圆曲线的基本形式是

这样的线性系定义了一个该曲线到射影直线上的二次态射。超椭圆曲线的亏格为

当n=1时是射影直线；

当n=3时是椭圆曲线，按惯例亏格0和1的曲线不称为超椭圆曲线。

在亏格

美国华盛顿大学教授Neal Koblitz首先发明了超椭圆曲线密码。超椭圆曲线密码是利用超椭圆曲线C的Jacobian上的离散对数问题(HECDLP)的“不可行性”。但是只有亏格为2的超椭圆曲线密码的安全性能和椭圆曲线密码的安全性媲美。无论是域K过小或者亏格g过大都会使得超椭圆曲线密码不安全。