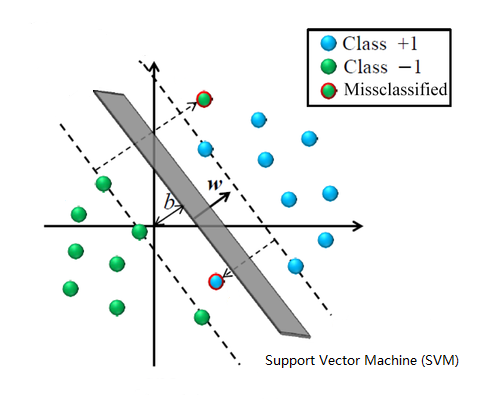
支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据进行二元分类的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplane）。SVM使用铰链损失函数（hinge loss）计算经验风险（empirical risk）并在求解系统中加入了正则化项以优化结构风险（structural risk），是一个具有稀疏性和稳健性的分类器。SVM可以通过核方法（kernel method）进行非线性分类，是常见的核学习（kernel learning）方法之一。

中文名：支持向量机

外文名：Support Vector Machine, SVM

类型：机器学习算法

提出者：V.N. Vapnik，A.Y. Chervonenkis，C. Cortes 等

提出时间：1964年

学科：统计学，人工智能

应用：计算机视觉，自然语言处理，生物信息学

SVM是由模式识别中广义肖像算法（generalized portrait algorithm）发展而来的分类器 ，其早期工作来自前苏联学者Vladimir N. Vapnik和Alexander Y. Lerner在1963年发表的研究 。1964年，Vapnik和Alexey Y. Chervonenkis对广义肖像算法进行了进一步讨论并建立了硬边距的线性SVM 。此后在二十世纪70-80年代，随着模式识别中最大边距决策边界的理论研究 、基于松弛变量（slack variable）的规划问题求解技术的出现 ，和VC维（Vapnik-Chervonenkis dimension, VC dimension）的提出 ，SVM被逐步理论化并成为统计学习理论的一部分 。1992年，Bernhard E. Boser、Isabelle M. Guyon和Vapnik通过核方法得到了非线性SVM 。1995年，Corinna Cortes和Vapnik提出了软边距的非线性SVM并将其应用于手写字符识别问题 ，这份研究在发表后得到了关注和引用，为SVM在各领域的应用提供了参考。

线性分类

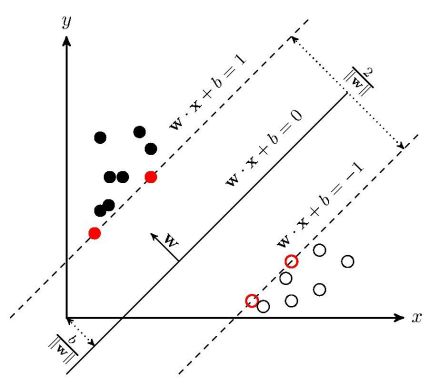线性可分：决策边界（实），间隔边界（虚），支持向量（红点）

在分类问题中给定输入数据和学习目标：

%20，而学习目标为二元变量

%20表示负类（negative%20class）和正类（positive%20class）。

若输入数据所在的特征空间存在作为决策边界（decision%20boundary）的超平面将学习目标按正类和负类分开，并使任意样本的点到平面距离大于等于1%20：

%20则称该分类问题具有线性可分性，参数

%20分别为超平面的法向量和截距。

满足该条件的决策边界实际上构造了2个平行的超平面作为间隔边界以判别样本的分类：

%20所有在上间隔边界上方的样本属于正类，在下间隔边界下方的样本属于负类。两个间隔边界的距离

%20被定义为边距（margin），位于间隔边界上的正类和负类样本为支持向量（support%20vector）。

0-1损失函数和其代理损失，红实线为0-1损失，黑实线为铰链损失。

损失函数（loss function）

在一个分类问题不具有线性可分性时，使用超平面作为决策边界会带来分类损失，即部分支持向量不再位于间隔边界上，而是进入了间隔边界内部，或落入决策边界的错误一侧。损失函数可以对分类损失进行量化，其按数学意义可以得到的形式是0-1损失函数：

%200-1损失函数不是连续函数，不利于优化问题的求解，因此通常的选择是构造代理损失（surrogate%20loss）。可用的选择包括铰链损失函数（hinge%20loss）、logistic损失函数（logistic%20loss）、和指数损失函数（exponential%20loss），其中SVM使用的是铰链损失函数%20：

对替代损失的相合性研究表明，当代理损失是连续凸函数，并在任意取值下是0-1损失函数的上界，则求解代理损失最小化所得结果也是0-1损失最小化的解%20%20。铰链损失函数满足上述条件。

经验风险（empirical%20risk）与结构风险（structural%20risk）

参见：统计学习理论

按统计学习理论，分类器在经过学习并应用于新数据时会产生风险，风险的类型可分为经验风险和结构风险%20：

式中

表示分类器，经验风险由损失函数定义，描述了分类器所给出的分类结果的准确程度；结构风险由分类器参数矩阵的范数定义，描述了分类器自身的复杂程度以及稳定程度，复杂的分类器容易产生过拟合，因此是不稳定的。若一个分类器通过最小化经验风险和结构风险的线性组合以确定其模型参数：

%20则对该分类器的求解是一个正则化问题，常数

%20是正则化系数。当

%20时，该式被称为L2正则化或Tikhonov正则化（Tikhonov%20regularization）%20。SVM的结构风险按

表示，在线性可分问题下，硬边界SVM的经验风险可以归0，因此其是一个完全最小化结构风险的分类器；在线性不可分问题中，软边界SVM的经验风险不可归0，因此其是一个L2正则化分类器，最小化结构风险和经验风险的线性组合。

核方法

主条目：核方法

一些线性不可分的问题可能是非线性可分的，即特征空间存在超曲面（hypersurface）将正类和负类分开。使用非线性函数可以将非线性可分问题从原始的特征空间映射至更高维的希尔伯特空间（Hilbert%20space）

%20，从而转化为线性可分问题，此时作为决策边界的超平面表示如下%20：

%20式中

%20为映射函数。由于映射函数具有复杂的形式，难以计算其内积，因此可使用核方法（kernel%20method），即定义映射函数的内积为核函数（kernel%20function）：

%20以回避内积的显式计算%20。

Mercer定理（Mercer's%20theorem）

核函数的选择需要一定条件，函数

%20是核函数的充要条件是，对输入空间的任意向量：

%20，其核矩阵（kernel%20matrix），即如下形式的格拉姆矩阵（Gram%20matrix）：

%20是半正定矩阵。上述结论被称为Mercer定理%20%20。定理的证明从略，结论性地，作为充分条件：特征空间内两个函数的内积是一个二元函数，在其核矩阵为半正定矩阵时，该二元函数具有可再生性：

%20，因此其内积空间是一个赋范向量空间（normed%20vector%20space），可以完备化得到希尔伯特空间%20，即再生核希尔伯特空间（Reproducing%20Kernel%20Hilbert%20Space,%20RKHS）。作为必要条件，对核函数构造核矩阵后易知：

%20%20。

常见的核函数

在构造核函数后，验证其对输入空间内的任意格拉姆矩阵为半正定矩阵是困难的，因此通常的选择是使用现成的核函数%20。以下给出一些核函数的例子，其中未做说明的参数均是该核函数的超参数（hyper-parameter）%20：

名称

解析式

多项式核（polynomial%20kernel）

径向基函数核（RBF%20kernel）

拉普拉斯核（Laplacian%20kernel）

Sigmoid核（Sigmoid%20kernel）

当多项式核的阶为1时，其被称为线性核，对应的非线性分类器退化为线性分类器。RBF核也被称为高斯核（Gaussian%20kernel），其对应的映射函数将样本空间映射至无限维空间。核函数的线性组合和笛卡尔积也是核函数，此外对特征空间内的函数

%20，

%20也是核函数%20。

标准算法

线性SVM（linear%20SVM）

1.%20硬边距（hard%20margin）

给定输入数据和学习目标：

%20。注意到虽然超平面法向量

%20是唯一优化目标，但学习数据和超平面的截距通过约束条件影响了该优化问题的求解%20。硬边距SVM是正则化系数取0时的软边距SVM，其对偶问题和求解参见软边距SVM，这里不额外列出。

2.%20软边距（soft%20margin）

在线性不可分问题中使用硬边距SVM将产生分类误差，因此可在最大化边距的基础上引入损失函数构造新的优化问题。SVM使用铰链损失函数，沿用硬边界SVM的优化问题形式，软边距SVM的优化问题有如下表示：

%20上式表明可知，软边距SVM是一个L2正则化分类器，式中

%20表示铰链损失函数。使用松弛变量：

%20处理铰链损失函数的分段取值后，上式可化为：

%20求解上述软边距SVM通常利用其优化问题的对偶性（duality），这里给出推导：

定义软边距SVM的优化问题为原问题（primal%20problem），通过拉格朗日乘子（Lagrange%20multiplier）：

%20可得到其拉格朗日函数%20%20：

%20令拉格朗日函数对优化目标

%20的偏导数为0，可得到一系列包含拉格朗日乘子的表达式%20%20：

%20将其带入拉格朗日函数后可得原问题的对偶问题（dual%20problem）%20%20：

%20对偶问题的约束条件中包含不等关系，因此其存在局部最优的条件是拉格朗日乘子满足Karush-Kuhn-Tucker条件（Karush-Kuhn-Tucker%20condition,%20KKT）%20：

由上述KKT条件可知，对任意样本

%20，总有

%20或

%20，对前者，该样本不会对决策边界

%20产生影响，对后者，该样本满足

%20意味其处于间隔边界上（

%20）、间隔内部（

%20）或被错误分类（

%20），即该样本是支持向量。由此可见，软边距SVM决策边界的确定仅与支持向量有关，使用铰链损失函数使得SVM具有稀疏性%20。

非线性SVM（nonlinear%20SVM）

使用非线性函数将输入数据映射至高维空间后应用线性SVM可得到非线性SVM。非线性SVM有如下优化问题%20：

%20类比软边距SVM，非线性SVM有如下对偶问题%20：

%20注意到式中存在映射函数内积，因此可以使用核方法，即直接选取核函数：

%20。非线性SVM的对偶问题的KKT条件可同样类比软边距线性SVM。

数值求解

SVM的求解可以使用二次凸优化问题的数值方法，例如内点法和序列最小优化算法，在拥有充足学习样本时也可使用随机梯度下降。这里对以上3种数值方法在SVM中的应用进行介绍。

1.%20内点法（Interior%20Point%20Method,%20IPM）

以软边距SVM为例，IPM使用对数阻挡函数（logarithmic%20barrier%20function）将SVM的对偶问题由极大值问题转化为极小值问题并将其优化目标和约束条件近似表示为如下形式%20：

%20式中

%20为对数阻挡函数，在本质上是使用连续函数对约束条件中的不等关系进行近似。对任意超参数

%20，使用牛顿迭代法（Newton-Raphson%20method）可求解

%20，该数值解也是原对偶问题的近似解：

%20。

IPM在计算

%20时需要对N阶矩阵求逆，在使用牛顿迭代法时也需要计算Hessian矩阵的逆，是一个内存开销大且复杂度为

%20的算法，仅适用于少量学习样本的情形%20。一些研究通过低秩近似（low-rank%20approximation）和并行计算提出了更适用于大数据的IPM，并在SVM的实际学习中进行了应用和比较%20。

2.%20序列最小优化（Sequential%20Minimal%20Optimization,%20SMO）

SMO是一种坐标下降法（coordinate%20descent），以迭代方式求解SVM的对偶问题，其设计是在每个迭代步选择拉格朗日乘子中的两个变量

%20并固定其它参数，将原优化问题化简至1维子可行域（feasible%20subspace），此时约束条件有如下等价形式%20：

%20将上式右侧带入SVM的对偶问题并消去求和项中的

%20可以得到仅关于

%20的二次规划问题，该优化问题有闭式解可以快速计算。在此基础上，SMO有如下计算框架%20：

1.

初始所有化拉格朗日乘子；

2.

识别一个不满足KKT条件的乘子，并求解其二次规划问题；

3.

反复执行上述步骤直到所有乘子满足KKT条件或参数的更新量小于设定值。

可以证明，在二次凸优化问题中，SMO的每步迭代都严格地优化了SVM的对偶问题，且迭代会在有限步后收敛于全局极大值%20。SMO算法的迭代速度与所选取乘子对KKT条件的偏离程度有关，因此SMO通常采用启发式方法选取拉格朗日乘子%20。

3.%20随机梯度下降（Stochastic%20Gradient%20Descent,%20SGD）

SGD是机器学习问题中常见的优化算法，适用于样本充足的学习问题。SGD每次迭代都随机选择学习样本更新模型参数，以减少一次性处理所有样本带来的内存开销，其更新规则如下%20：

%20式中梯度前的系数是学习速率（learning%20rate），

%20是代价函数（cost%20function）。由于SVM的优化目标是凸函数，因此可以直接将其改写为极小值问题并作为代价函数运行SGD。以非线性SVM为例，其SGD迭代规则如下%20：

%20由上式可知，在每次迭代时，SGD首先判定约束条件，若该样本不满足约束条件，则SGD按学习速率最小化结构风险；若该样本满足约束条件，为SVM的支持向量，则SGD根据正则化系数平衡经验风险和结构风险，即SGD的迭代保持了SVM的稀疏性。

编程实现

这里提供一个python%203环境下使用scikit-learn封装模块的SVM编程实现：

# 导入模块 import numpy as np import matplotlib.pyplot as plt from sklearn import svm, datasets % matplotlib inline # 鸢尾花数据 iris = datasets.load_iris() X = iris.data # 为便于绘图仅选择2个特征 y = iris.target # 测试样本（绘制分类区域） xlist1 = np.linspace(X.min(), X.max(), 200) xlist2 = np.linspace(X.min(), X.max(), 200) XGrid1, XGrid2 = np.meshgrid(xlist1, xlist2) # 非线性SVM：RBF核，超参数为0.5，正则化系数为1，SMO迭代精度1e-5, 内存占用1000MB svc = svm.SVC(kernel='rbf', C=1, gamma=0.5, tol=1e-5, cache_size=1000).fit(X, y) # 预测并绘制结果 Z = svc.predict(np.vstack().T) Z = Z.reshape(XGrid1.shape) plt.contourf(XGrid1, XGrid2, Z, cmap=plt.cm.hsv) plt.contour(XGrid1, XGrid2, Z, colors=('k',)) plt.scatter(X, X, c=y, edgecolors='k', linewidth=1.5, cmap=plt.cm.hsv)

改进算法

偏斜数据的改进算法

软边距的线性和非线性SVM可以通过修该其正则化系数为偏斜数据赋权。具体地，若学习样本中正例的数量远大于负例，则可按样本比例设定正则化系数%20：

%20式中的

%20表示正例和负例，即在正例多时，对正利使用小的正则化系数，使SVM倾向于通过正例降低结构风险，同时也对负例使用大的正则化系数，使SVM倾向于通过负例降低经验风险。

概率SVM（Platt's%20probabilistic%20outputs）

概率SVM可以视为Logistic回归和SVM的结合，SVM由决策边界直接输出样本的分类，概率SVM则通过Sigmoid函数计算样本属于其类别的概率%20。具体地，在计算标准SVM得到学习样本的决策边界后，概率SVM通过缩放和平移参数

%20对决策边界进行线性变换，并使用极大似然估计（Maximum%20Liklihood%20Estimation,%20MLE）得到

%20的值，将样本到线性变换后超平面的距离作为Sigmoid函数的输入得到概率%20。在通过标准SVM求解决策边界后，概率SVM的改进可表示如下%20：

%20式中第一行的优化问题实际上是缩放和平移参数的Logistic回归，需要使用梯度下降算法求解，这意味着概率SVM的运行效率低于标准SVM%20。在通过学习样本得到缩放和平移参数的MLE后，将参数应用于测试样本可计算SVM的输出概率。

多分类SVM（multiple%20class%20SVM）

标准SVM是基于二元分类问题设计的算法，无法直接处理多分类问题。利用标准SVM的计算流程有序地构建多个决策边界以实现样本的多分类，通常的实现为“一对多（one-against-all）”和“一对一（one-against-one）”%20。一对多SVM对m个分类建立m个决策边界，每个决策边界判定一个分类对其余所有分类的归属；一对一SVM是一种投票法（voting），其计算流程是对m个分类中的任意2个建立决策边界，即共有

%20个决策边界，样本的类别按其对所有决策边界的判别结果中得分最高的类别选取%20。一对多SVM通过对标准SVM的优化问题进行修改可以实现一次迭代计算所有决策边界%20。

最小二乘SVM（Least%20Square%20SVM,%20LS-SVM）

LS-SVM是标准SVM的一种变体，两者的差别是LS-SVM没有使用铰链损失函数，而是将其优化问题改写为类似于岭回归（ridge%20regression）的形式，对软边距SVM，LS-SVM的优化问题如下%20：

%20类比标准SVM，可以通过拉格朗日乘子：

%20得到LS-SVM的对偶问题，该对偶问题是一个线性系统%20：

双螺旋分类实例，阴影为LS-SVM的分类结果

%20上述公式可以使用核方法得到非线性LS-SVM%20。LS-SVM的线性系统可以通过共轭梯度法（conjugate%20gradient）或SMO求解%20，且求解效率通常高于标准SVM的二次凸优化问题%20。研究表明，对任意维度的特征空间，当样本间线性独立（linearly%20independent）时，LS-SVM和SVM会得到相同的结果%20，若该条件不满足，则二者的输出是不同的。一个对二者进行比较的例子是双螺旋分类（two-spiral%20classification）%20。

结构化SVM（structured%20SVM）

结构化SVM是标准SVM在处理结构化预测（structured%20prediction）问题时所得到的推广，给定样本空间和标签空间的结构化数据

%20和标签空间内的距离函数

%20，其优化问题如下：

%20结构化SVM被应用于自然语言处理（Natural%20Language%20Processing,%20NLP）问题中，例如给定语料库数据对其语法分析器（parser）的结构进行预测%20，也被用于生物信息学（bioinformatics）中的蛋白质结构预测（protein%20structure%20prediction）%20。

多核SVM（multiple%20kernel%20SVM）

多核SVM是多核学习（multiple%20kernel%20learning）在监督学习中的实现，是在标准的非线性SVM中将单个核函数替换为核函数族（kernel%20family）的改进算法。多核SVM的构建方法可以被归纳为以下5类%20：

1.

显式规则（fixed%20rule）：在不加入任何超参数的情形下使用核函数的性质，例如线性可加性构建核函数族。显示规则构建的多核SVM可以直接使用标准SVM的方法进行求解。

2.

启发式方法（heuristic%20approach）：使用包含参数的组合函数构建核函数族，参数按参与构建的单个核函数的核矩阵或分类表现确定。

3.

优化方法（optimization%20approach）：使用包含参数的组合函数构建核函数族，参数按核函数间的相似性或最小化结构风险或所得到的优化问题求解。

4.

贝叶斯方法（Bayesian%20approach）：使用包含参数的组合函数构建核函数族，参数被视为随机变量并按贝叶斯推断方法进行估计。

5.

提升方法（Boosting%20approach）：按迭代方式不断在核函数族中加入核函数直到多核SVM的分类表现不再提升为止。

研究表明，从分类的准确性而言，多核SVM具有更高的灵活性，在总体上也优于使用其核函数族中某个单核计算的标准SVM，但非线性和依赖于样本的核函数族构建方法不总是更优的。核函数族的构建通常依具体问题而定%20。

扩展算法

支持向量回归（Support%20Vector%20Regression,%20SVR）

将SVM由分类问题推广至回归问题可以得到支持向量回归（Support%20Vector%20Regression,%20SVR），此时SVM的标准算法也被称为支持向量分类（Support%20Vector%20Classification,%20SVC）%20%20。SVC中的超平面决策边界是SVR的回归模型：

%20。SVR具有稀疏性，若样本点与回归模型足够接近，即落入回归模型的间隔边界内，则该样本不计算损失，对应的损失函数被称为ε-不敏感损失函数（ε-insensitive%20loss）：

%20，其中

%20是决定间隔边界宽度的超参数%20。可知，不敏感损失函数与SVC使用的铰链损失函数相似，在原点附近的部分取值被固定为0。类比软边距SVM，SVR是如下形式的二次凸优化问题%20：

%20使用松弛变量

%20表示ε-不敏感损失函数的分段取值后可得%20：

%20类似于软边距SVM，通过引入拉格朗日乘子：

%20可得到其拉格朗日函数和对偶问题%20：

%20其中对偶问题有如下KKT条件%20：

%20对该对偶问题进行求解可以得到SVR的形式为%20：

%20SVR可以通过核方法得到非线性的回归结果%20。此外LS-SVM可以按与SVR相似的方法求解回归问题%20。

支持向量聚类（support%20vector%20clustering）

使用RBF核和不同超参数的支持向量聚类实例。

支持向量聚类是一类非参数的聚类算法，是SVM在聚类问题中的推广。具体地，支持向量聚类首先使用核函数，通常是径向基函数核，将样本映射至高维空间，随后使用SVDD（Support Vector Domain Description）算法得到一个闭合超曲面作为高维空间中样本点富集区域的刻画。最后，支持向量聚类将该曲面映射回原特征空间 ，得到一系列闭合等值线，每个等值线内部的样本会被赋予一个类别 。

支持向量聚类不要求预先给定聚类个数，研究表明，支持向量聚类在低维学习样本的聚类中有稳定表现，高维样本通过其它降维（dimensionality reduction）方法进行预处理后也可进行支持向量聚类 。

半监督SVM（Semi-Supervised SVM, S3VM）

S3VM是SVM在半监督学习中的应用，可以应用于少量标签数据和大量无标签数据组成的学习样本。在不考虑未标记样本时，SVM会求解最大边距超平面，在考虑无标签数据后，S3VM会依据低密度分隔（low density separation）假设求解能将两类标签样本分开，且穿过无标签数据低密度区域的划分超平面。

S3VM的一般形式是按标准SVM的方法从标签数据中求解决策边界，并通过探索无标签数据对决策边界进行调整。在软边距SVM的基础上，S3VM的优化问题另外引入了2个松弛变量 ：

式中

为有标签和无标签样本的个数，松弛变量

表示S3VM将无标签数据归入两个类别产生的经验风险。

S3VM有很多变体，包括直推式SVM（Transductive SVM, TSVM） 、拉普拉斯SVM（Laplacian SVM）和均值S3VM（mean S3VM） 。

与其它线性分类器的关系：SVM是一个广义线性分类器，通过在SVM的算法框架下修改损失函数和优化问题可以得到其它类型的线性分类器，例如将SVM的损失函数替换为logistic损失函数就得到了接近于logistic回归的优化问题 。SVM和logistic回归是功能相近的分类器，二者的区别在于logistic回归的输出具有概率意义，也容易扩展至多分类问题，而SVM的稀疏性和稳定性使其具有良好的泛化能力并在使用核方法时计算量更小 。

作为核方法的性质：SVM不是唯一可以使用核技巧的机器学习算法，logistic回归、岭回归和线性判别分析（Linear DiscriminantAnalysis, LDA）也可通过核方法得到核logistic回归（kernel logistic regression）、核岭回归（kernel ridge regression）和核线性判别分析（Kernelized LDA, KLDA）方法。因此SVM是广义上核学习的实现之一 。

包含SVM的编程模块

按引用次数，由台湾大学资讯工程研究所开发的LIBSVM是使用最广的SVM工具 。LIBSVM包含标准SVM算法、概率输出、支持向量回归、多分类SVM等功能，其源代码由C编写，并有JAVA、Python、R、MATLAB等语言的调用接口、基于CUDA的GPU加速和其它功能性组件，例如多核并行计算、模型交叉验证等 。

基于Python开发的机器学习模块scikit-learn提供预封装的SVM工具，其设计参考了LIBSVM 。其它包含SVM的Python模块有MDP 、MLPy 、PyMVPA 等。TensorFlow的高阶API组件Estimators有提供SVM的封装模型 。